Дії з одиницями вимірювання

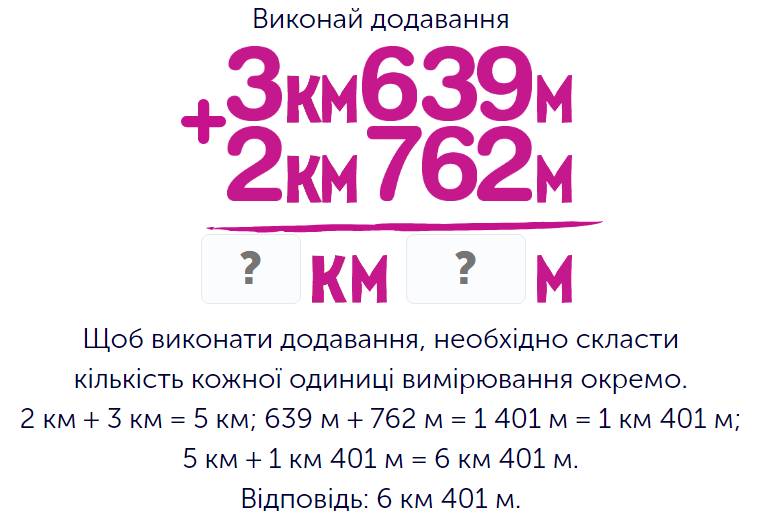
Одиниці вимірювання, які належать до однієї системи та присвячені вимірювання одної характеристики, можуть взаємодіяти між собою. Наприклад, метри переводяться у кілометри, а мілілітри – в літри. Відповідно, у одному прикладі можуть бути кілометри з метрами (а також сантиметри з дециметрами, але це означатиме більшу складність виразу у звʼязку з наявністю більш віддалених одне від одного числових значень), а кілограми з грамами. На кожному етапі завдання перед учнем буде зображення одного прикладу, де містяться різні одиниці вимірювання, які витримані в рамках цього правила. Учень вивчає водночас і числові значення, і описану дію (додавання ,віднімання, множення та ділення) і одиниці вимірювання, що було тут задіяно. Наприклад, до пʼяти кілометрів двадцяти метрів треба додати «980 метрів». Учень додає метри окремо, згадуючи, що тисяча метрів – то вже, власне, кілометр, від так відповіддю на цей вираз буде «6 кілометрів» рівно. Коли дитина вводить правильні числові значення у каркас відповіді, де вже містяться умовні позначення, то проходить на наступний етап завдання. Ця вправа є досить легкою, адже дитина буде працювати здебільшого з невеликими числами, а в прикладі всього лише два елемента. Однак, вона є дуже важливою для того, щоб школяр навчився правильно співвідносити одиниці вимірювання, тримаючи в памʼяті, скільки метрів «поміщається» в кілометрі тощо. Таким чином, саме завдяки практичній спрямованості цього завдання досягається більш ефективне тренування навичок роботи з одиниця вимірювання. Крім того, школяр краще розуміє, наскільки відокремленими одне від одного є ті одиниці, що описують зовсім різні параметри на кшталт обʼєму та довжини або ваги та відстані.