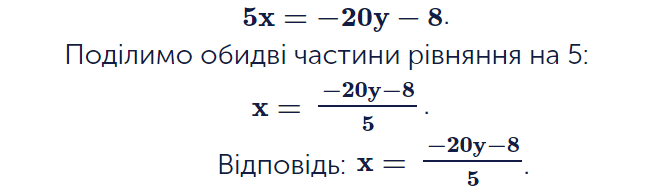Опис завдання
Рівняння, у якому є дві змінні, подається здебільшого як приклад, де літери грають роль невідомих елементів. Але більшість таких рівнянь цілком можна переробити таким чином, щоб одну змінну можна було виразити через іншу. Наприклад, «45х+у=10» можна переробити на «у=10–45х».
Перед учнем міститься рівняння з кількома різними діями та двома змінними. Відомо, чому дорівнює цей вираз. Школяр має скористатися взаємодією між різними компонентами рівняння для того, що через одну змінну виразити іншу. Початковий вигляд рівняння подається у формулюванні завдання. Нижче є каркас цього ж рівняння в переробленому вигляді. Цей каркас є частиною ілюстрації. Дитина має зрозуміти, як мусять взаємодіяти числа та змінна, щоб виразити іншу змінну: де потрібно використати спосіб знаходження невідомого множника, де — відшукати невідомий дільник тощо.
Ця вправа дозволяє дитині глибоко проникнути в розуміння структури рівняння та того, чим для різних його компонентів може бути та чи інша змінна.
Пов'язані стандарти
Учень/учениця пояснює, що таке: аргумент; функція; область визначення функції; область значень функції; графік функції.
Учень/учениця розв’язує вправи, що передбачають: знаходження області визначення функції; знаходження значення функції за даним значенням аргументу; побудову графіка лінійної функції; знаходження за графіком функції значення функції за даним значенням аргументу і навпаки; визначення окремих характеристик функції за її графіком (додатні значення, від’ємні значення, нулі).
Учень/учениця наводить приклади: рівняння з однією та двома змінними; лінійних рівнянь з однією та двома змінними; системи двох лінійних рівнянь з двома змінними.