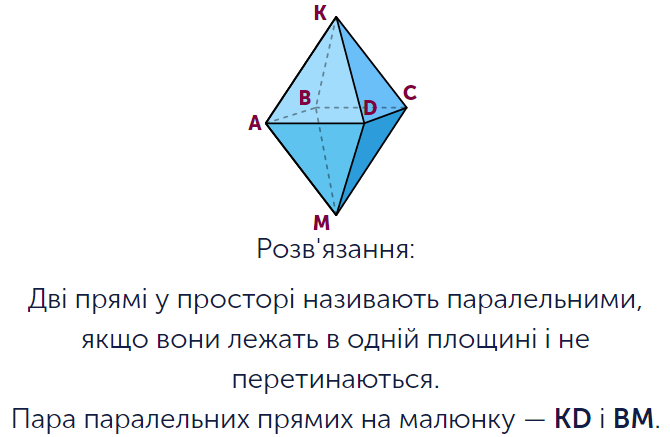
Опис завдання
У цій вправі з курсу ЗНО з математики тренуємо важливу тему «Паралельність у просторі» через коротке, але змістовне запитання з геометрії. На зображенні подано фігуру F, що складається з 5 точок. Потрібно визначити, скільки точок може мати паралельна проекція цієї фігури, обравши правильний варіант із запропонованих: 5, 6, 7 або 10.
Завдання допомагає зрозуміти, як працює паралельна проекція: що саме зберігається під час проєктування, а що може змінюватися. Учень вчиться уважно читати умову, аналізувати геометричний зміст поняття «проекція» та робити логічний висновок, не підміняючи його здогадками. Такий формат зручний для швидкого самоконтролю й повторення перед тестуванням.
Вправа стане корисною і для школярів, які готуються до ЗНО/НМТ, і для вчителів, які добирають лаконічні завдання на закріплення теми, і для батьків, що хочуть зрозуміти, над чим саме працює дитина. Тут важливо не лише «вгадати» відповідь, а пояснити собі, чи може проекція зберегти кількість точок, чи в окремих випадках різні точки можуть спроєктуватися в одну.
- Розвиває просторове мислення та вміння працювати з геометричними перетвореннями.
- Тренує логіку й уважність: потрібно обрати правильну кількість точок у проекції з кількох варіантів.
- Допомагає систематизувати знання з теми паралельності та проєктування у просторі.
- Підходить для самостійної підготовки до ЗНО/НМТ і для короткої перевірки на уроці.
Learning.ua пропонує вправи, які легко вписати в щоденну підготовку: кілька хвилин на одне завдання — і ви поступово закріплюєте ключові поняття. Виконуйте вправу, перевіряйте себе та повертайтеся до теми стільки разів, скільки потрібно, щоб упевнено розв’язувати подібні задачі на іспиті.
Пов'язані стандарти
Учасник/учасниця ЗНО повинен/повинна вміти:
- застосовувати означення та властивості паралельних і перпендикулярних прямих і площин до розв'язування стереометричних задач та задач практичного змісту;
- знаходити зазначені відстані та величини кутів у просторі.