Зовсім нещодавно наша команда поділилася з вами неймовірними новинам! Тепер на нашому сайті учні 9-х класів можуть проходити повноцінний курс із математики. Про його головні особливості та варіанти завдань ми розповідаємо у цьому огляді.
Основні характеристики курсу:
- Новий рівень повністю відповідає стандартам МОН України, а також стандартам міжнародного зразку — Common Core.
- Певні завдання мають спеціальні позначки — прапорці. Помаранчевий вказує на завдання з поглибленим вивченням математики, зелений — вправа відповідає тільки міжнародним стандартам.
- Курс містить 300 окремих вправ та 35 повноцінних тем.
- Новий рівень розрахований на учнів 14-15 років. Долучитися до курсу можуть й 8-класники, які відчувають у собі достатньо сил для проходження рівня, а також учні 10-х класів для того, щоб надолужити певні знання.
Що залишається незмінним?
Є речі, які існуватимуть завжди :) Такою є система бонусів від Learning.ua. За кожний вдало виконаний блок завдань наші учні отримають приємні подарунки від сайту. Це можуть бути наліпки, логічні задачки, спеціальні нагороди тощо. Звісно, система вдосконалюється для 9-класників, щоб бути цікавою та відповідати інтересам учнів.
Слідкувати за прогресом в особистому кабінеті школяра можуть батьки, вчителі та сам учень. Саме там доступна статистика проходження вправ, яка допоможе корелювати проходження курсу для 9-класника. Крім того, там можна переглянути, які вправи давались дитині найкраще, а які треба буде пройти ще кілька разів.
А тепер пропонуємо перейти безпосередньо до вправ! Адже це — найцікавіша частина огляду.
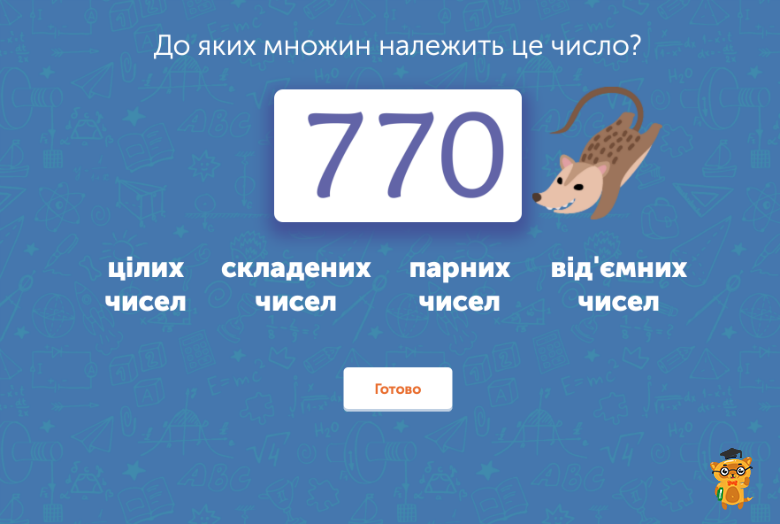
Вивчення математики 9-го класу розпочинається із алгебри, а саме — із дослідження чисел та їхніх видів. Існує цілий комплекс характеристик, за яким ми можемо оцінювати числа. Так, наприклад, вони можуть бути натуральними, цілими, раціональними, ірраціональними, додатними та від’ємними, парними або ні, простими, складними, складеними тощо. Загубитися серед такої кількості визначень справді легко. Тому наша перша тема курсу спрямована на те, щоб допомогти 9-класнику раз і назавжди розставити всі крапки над «і» у вивченні цієї теми.
У цьому завданні учень має уважно дослідити представлене число та вказати, до яких множин воно може належати. Наприклад, число 770 — парне, складне, ціле.

Це завдання знаходиться у темі «Буквені вирази та нерівності». А отже, школяр розпочинає активне знайомство та роботу з числовими нерівностями. Це досить значна тема, яка з кожним кроком вивчення буде розширюватися та ускладнюватися у своїх властивостях. Однак на цьому етапі проходження завдань головне, що має зрозуміти учень під час проходження подібних вправ, — те, що нерівності здатні мати одразу кілька правильних розв’язків. Оскільки раніше учні працювали переважно з рівняннями, то подібний факт може дещо збивати з пантелику. Наша гра «Кмітливі клоуни» дозволить дітям активно потренувати всі можливі варіанти розв’язків нерівностей.

Досить цікава задача, яка нагадує нам про вивчення відсотків. Ця тема існує на кожному курсі, адже є незамінною на практиці. Майже кожного дня дорослі та діти стикаються з необхідністю рахувати відсотки, а тому їхнє розуміння є вкрай важливим. На цьому етапі проходження завдань школяр зможе розглянути відсотки у контексті дослідження хімічних сплавів. Це ще раз говорить про всебічність та інтерактивність завдань курсу. Головна мета учня — уважно розглянути надані числа, порахувати можливий відсоток від числа або ж число за його відсотком, надати відповідь щодо відсоткового відношення домішків у сплаві.

Квадратні рівняння, мабуть, — одна із найважливіших та провідних тем у вивченні алгебри 9 класів. Під час розгляду цієї теми учень стикнеться із такими важливими моментами, як-от рівносильні та неповні квадратні рівняння, зведення звичайного до квадратного, пошук дискримінанту, знаходження коренів, їхньої суми та добутку, додатні та від’ємні корені, визначення коефіцієнтів рівняння, біквадратні рівняння та, звісно, теорема Вієта. Остання — це математична теорема, що виражає коефіцієнти багаточлена через його корені. Її особливість полягає у тому, що вона дозволяє не лише перевірити правильність розв’язання квадратного рівняння, а й працювати з таким виразом, що має визначені властивості.
Конкретно у цьому завданні школяр має розглянути квадратне рівняння, знайти суму та добуток його коренів, після чого визначити, які числа стануть розв’язком рівняння.

Для розв’язання системи рівнянь існує кілька варіантів для розгляду. Один із них — це вирішення системи рівнянь шляхом побудови графіків функцій та пошуку спільних точок перетину. Побудова графіків на координатній площині дещо спрощує процес пошуку коренів, адже школяр націлений не на те, щоб підставити необхідні числа та знайти корені, а на те, щоб побудувати функції та поглянути, які координати матимуть точки перетину. На нашу думку, такий спосіб надає рівнянням більшої інтерактивності та залученості зі сторони 9-класників. У цій вправі перед учнем вже є система та готовий графік функцій. Єдине, що треба зробити, — записати розв’язки в залежності від того, які наведено координати.
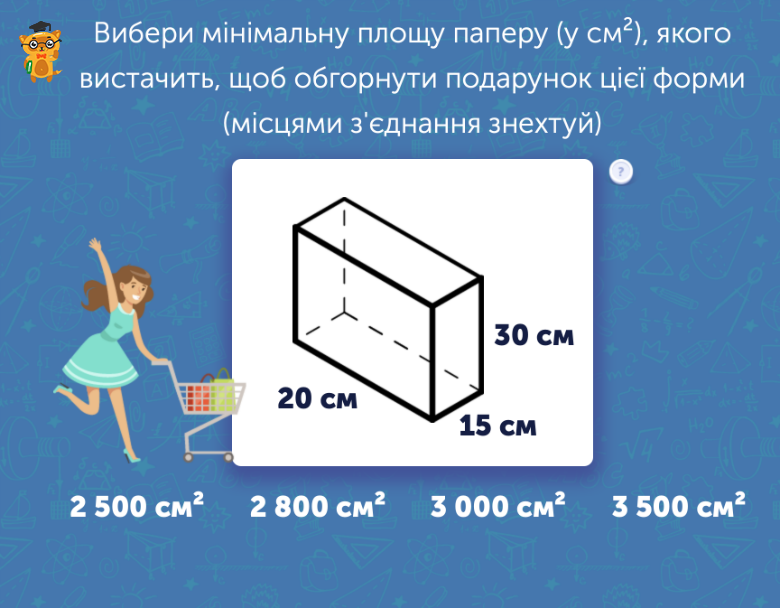
Прикладна математика — один із наших улюблених розділів на кожному курсі. Адже саме ця тема здатна відповісти на всі питання школяра та пояснити, навіщо він вивчає математику та де у реальному житті він зможе застосувати наявні знання. Вправа «Обгортаємо подарунок» — це перша можливість 9-класника стикнутися із геометрією та згадати базові властивості фігур. Так, наприклад, учень має перед собою прямокутну коробку, де відомі довжини усіх її сторін. Завдання, яке стоїть перед учнем, — порахувати, скільки святкового паперу необхідно для того, щоб повністю вкрити коробку. Чудова вправа перед новорічними святами!

Ще одна неймовірна вправа з розділу прикладної математики — «Порівнюємо ціни». Скоро свята, а тому магазини люблять говорити нам про чудові знижки та акції. Але от зрозуміти, чи дійсно акція або знижка варта уваги та працює, можливо, якщо уважно переглянути та порахувати наведені ціни. Наприклад, це завдання показує, що перед початком акцій власники, як правило, піднімають ціни і тільки після цього їх зменшують. Школяр має проаналізувати та порахувати у відсотковому співвідношенні, на скільки змінилась ціна після подорожчання та знижки, а потім вказати, чи дійсно акція працює і в ній є сенс. Тут учень знову зустрічається з відсотками, але вже бачить, як більш реально їх використати у житті.

Так, наша команда знає, що ми живемо у 21 столітті, а тому всім дітям добре відомо, що таке блог та блогери. У цьому й полягає важливість нашої онлайн-освіти — завдання мають відповідати не лише шкільній програмі та стандартам МОН України, але й інтересам самих учнів. У цій грі 9-класники розглянуть можливості та властивості геометричних прогресій. Нагадаємо, що геометрична прогресія — послідовність чисел, перший член якої не дорівнює нулю, а відношення будь-якого елемента послідовності до попереднього є сталим числом, що називається знаменником прогресії. Важливо також, щоб учень добре усвідомив — знаменник прогресії не може дорівнювати 1 (одиниці). У грі «Блог» школяр має визначити основні показники геометричної прогресії для того, щоб з’ясувати, скільки відео випустив блогер. Допоможуть у вирішенні завдання наведений перший член прогресії, знаменник та загальна кількість членів.

Формули скороченого множення — це часті випадки множення многочленів, що використовуються для розкладу многочленів на множники, для спрощення виразів, для зведення многочленів до стандартного вигляду. Всі формули скороченого множення доводяться безпосередньо розкриттям дужок і зведенням подібних доданків. Саме з цим доведеться попрацювати 9-класнику у наведеному завданні. Перед ним наявний вираз, який необхідно спростити. Для цього учень має використати власні знання про формули скороченого множення. Допоможуть у пошуці правильних відповідей й додаткові умови про різницю та добуток буквених виразів.
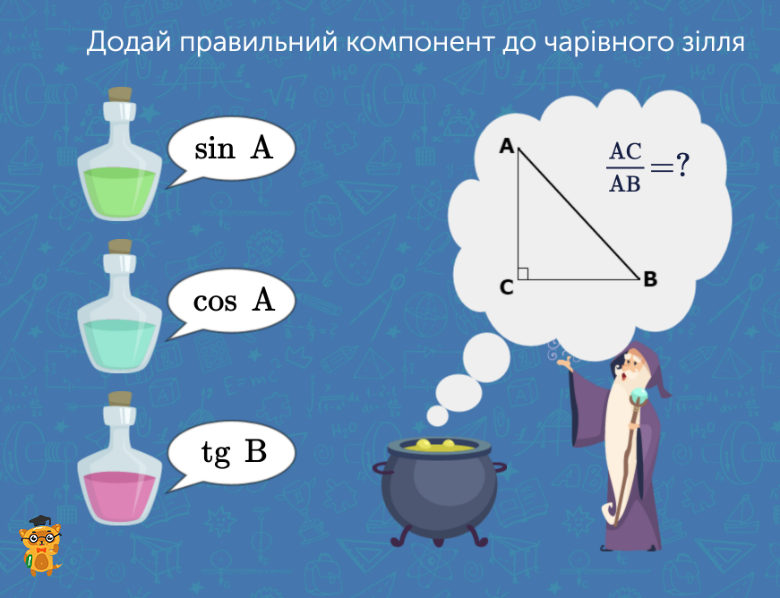
Нарешті переходимо до вивчення геометрії! І однією із найважливіших тем тут є тригонометрія та тригонометричні формули. Тригонометричні формули широко використовуються як в математиці, так і в фізиці. У математиці — при розв’язуванні трикутників, інтегруванні, в теорії функцій комплексних змінних і т. д. У фізиці — при розв’язуванні задач, у яких векторні величини не лежать на одній прямій. Отож, знання цієї теми є обов’язковим одразу для кількох точних наук. Завдання «Тригонометричне зілля» — одне з найпростіших із теми. Воно більше націлене на теоретичну базу, а саме — розуміння того, що означають базові поняття синусів, косинусів та тангенсів для прямокутного трикутника. Учень бачить перед собою співвідношення сторін та вказує, що воно означає.
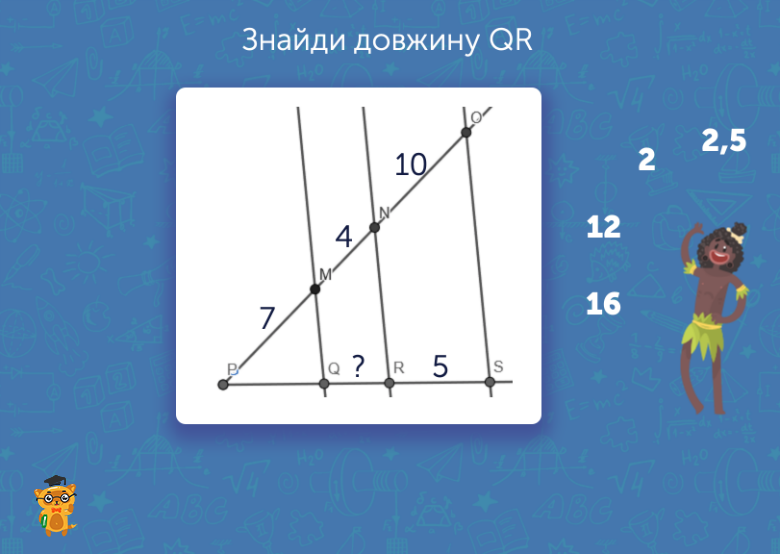
Під час розгляду цієї теми 9-класник з’ясує для себе, що таке теорема Фалеса, чому ті чи інші фігури можуть називатися подібними та які властивості вони повинні мати для цього. Крім того, учень розгляне можливості різних площ та фігур, дослідить узагальнену теорему Фалеса. Це чудова підготовка перед вивченням усіх наслідків із теореми та її доведенням. У цьому завданні перед школярем є одразу кілька трикутників та певні довжини сторін. Головне, що має з’ясувати учень, — чому дорівнює вказаний відрізок. Зробити це можна, згадавши основні аспекти теореми Фалеса.
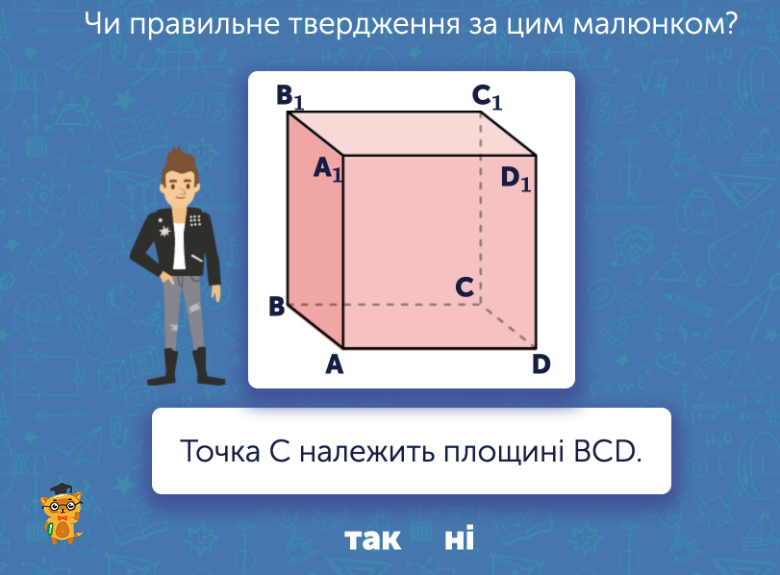
Геометрія — це значний розділ, який передбачає не тільки вивчення площ, об’ємів та периметрів фігур, але й вивчення площин. Школяр бачить перед собою об’ємні фігури, які має проаналізувати та зрозуміти, чи належить вказана в завданні точка тій площині, про яку говориться у вправі. Чудове завдання, аби тренувати уважність та логіку.
На цьому ми завершуємо наш огляд вправ 9-го класу з математики. Самі бачите — завдань багато, усі вони різні, яскраві, інтерактивні, прикладні. Важливо, що вони задовольняють потреби учня не тільки в знаннях, але й інтересах та зацікавленості. Тому долучайтесь до нашого нового рівня, щоб на власні очі побачити нові вправи та протестувати їх.
Нехай щастить!