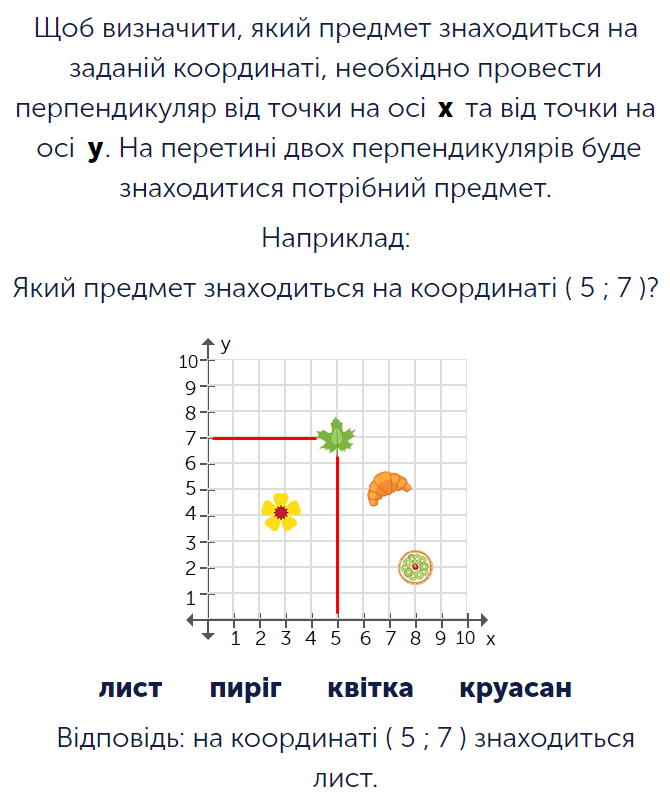
Опис завдання
Вправа «Предмет за координатою» допомагає тобі впевнено працювати з координатною сіткою. На екрані ти бачиш осі x та y, а також кілька предметів, розміщених у різних точках. Твоє завдання — знайти, який предмет стоїть на заданій координаті, наприклад (8; 3), і вибрати правильну відповідь серед запропонованих варіантів.
Такі завдання з математики для 5 класу навчають уважно читати координати. Перше число в дужках показує рух по осі x, тобто вправо. Друге число показує рух по осі y, тобто вгору. Якщо правильно поєднати ці два значення, ти знайдеш потрібну точку на сітці. Саме там буде зображений предмет: яблуко, груша, малина, гриб, апельсин або інший об’єкт.
Ця навчальна вправа корисна тим, що робить роботу з координатами на площині наочною і зрозумілою. Замість абстрактних точок ти бачиш знайомі малюнки. Це допомагає швидше зрозуміти, як працює координатна система, і не губитися, коли на полі є кілька об’єктів.
- Ти тренуєш уміння знаходити точку за координатами.
- Ти вчишся розрізняти осі x та y.
- Ти закріплюєш порядок запису координат у дужках.
- Ти розвиваєш уважність і просторове мислення.
- Ти готуєшся до складніших тем з математики.
Для батьків ця вправа є зручним способом підтримати дитину вдома. Можна попросити школяра пояснити свої дії: спочатку знайти число на осі x, потім число на осі y, а далі визначити предмет у точці перетину. Так дитина не просто натискає відповідь, а усвідомлює алгоритм розв’язання.
Для вчителів завдання може стати частиною уроку про координати на площині або коротким тренуванням після пояснення нової теми. Формат із предметами допомагає зацікавити учнів і швидко перевірити, чи розуміють вони, як читати координати. Вправа підходить для індивідуальної роботи, повторення та закріплення матеріалу.
Працюй спокійно й уважно. Пам’ятай: у координаті перше число відповідає осі x, а друге — осі y. Знайди потрібне місце на сітці, подивися, який предмет там розташований, і обери його назву. Крок за кроком ти навчишся легко орієнтуватися на координатній площині.
Пов'язані стандарти
Використовувати пару перпендикулярних числових прямих, які називаються осями, для визначення системи координат, з перетином прямих (початок координат), розташованих так, щоб вони співпали з 0 на кожній прямій і заданою точкою площини, розташованої за допомогою упорядкованої пари чисел, що називається її координатами. Усвідомити, що перше число вказує, наскільки далеко потрібно рухатися від початку в напрямку однієї осі, а друга цифра показує, наскільки далеко потрібно рухатися у напрямку другої осі, за умови, що назви двох осей та координат відповідні. (наприклад, x-осі та x-координаті, осі-y та координаті-y).
