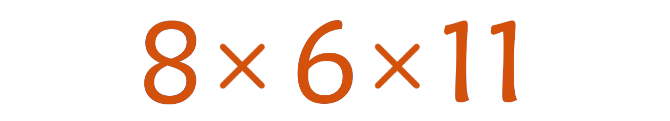Множення більш ніж двох чисел

Вивчення будь-якої теми у математиці відбувається за принципом «від простого до складного», тобто поступово, навіть якщо не змінюється характер опрацьованої дії, зростає складність конкретного випадку її застосування. Це цілком справедливо для множення: базові принципи виконання його незмінні, але приклади ускладнюються за рахунок зростання множників. Однак це – лише один із варіантів такого ускладнення. Інший варіант ускладнення, не менш важливий для практичного використання, це множення кількох чисел. У ході виконання цього завдання дитина множитиме як мінімум три числа в рамках одного прикладу. На екрані міститься зображення математичного прикладу з дією множення та трьома числами. Оскільки множити кілька чисел в межах одного виразу досить непросто, лише один із множників буде двоцифровим числом, тоді як пара інших – одноцифрові. Крім того, приклад надається у рядок, а не у стовпчик, без якихось додаткових підказок, які повʼязані зі структурою та послідовністю множення. Учень виконує дію множення послідовно: спочатку з однією парою чисел, а після цього перемножує добуток та останнє, третє число. При цьому дитина має можливість скористатись переставною властивістю множення. Переставна властивість множення стверджує, що від зміни множників місцями добуток не змінюється, як від зміни доданків не змінюється сума. Наприклад, вираз має такий вигляд: «8х3х21». Дитині простіше спочатку помножити трійку та число «21», а вже потім добуток множити на вісімку. Таким чином учень закріплює вміння користуватись властивостями множення на практиці. Коли школяр знаходиться правильну відповідь, то проходить на наступний етап завдання, де треба знайти добуток нового прикладу із трьома множниками.