Опис завдання
Знайти кут геометричної фігури не завжди легко. Іноді для цього необхідно використати іншу фігуру. Якщо взяти чотирикутник і провести лінію по його діагоналі, вийде два трикутника зі спільною стороною. Знаючи певні властивості кутів трикутників, уже можна знаходити невідомі кути початкової фігури. Це й робитиме дитина в процесі виконання цього завдання.
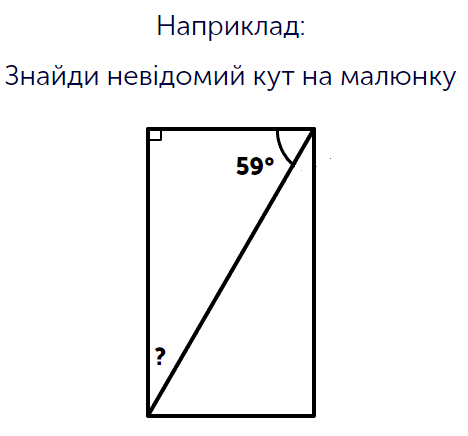
Перед учнем — чотирикутник, невідомий кут якого слід знайти через трикутники. Відомо, що сума всіх кутів трикутника завжди дорівнює 180 градусам. Якщо відомо, що один кут, скажімо, прямий, інший теж є відомим, то залишається знайти останній, віднявши від 180 суму двох відомих. На наступному етапі завдання подаватиметься вже інший подібний випадок, і різноманіття того, як трикутник може допомогти в роботі з чотирикутником має лише посилити цікавість учня до цієї теми.
Завдяки виконанню цього завдання дитина навчиться використовувати властивості однієї фігури для опрацювання інших, що робить знання геометрії не лише більш повним, а й більш практичним.
Пов'язані стандарти
Учень/учениця наводить приклади геометричних фігур, указаних у змісті.
Учень/учениця наводить приклади: геометричних фігур, указаних у змісті; рівних фігур.
Учень/учениця пояснює, що таке рівні фігури; формулює означення: зовнішнього кута трикутника; різних видів трикутників; бісектриси, висоти, медіани трикутника.
Учень/учениця класифікує трикутники за сторонами і за кутами.
Учень/учениця обґрунтовує: належність трикутника до певного виду; рівність трикутників.
Учень/учениця застосовує вивчені означення і властивості до розв’язування задач практичного змісту.
Учень/учениця формулює означення: зовнішнього кута трикутника.
Учень/учениця застосовує вивчені означення і властивості до розв’язування задач практичного змісту.
Учень/учениця застосовує вивчені означення і властивості до розв’язування задач, зокрема практичного змісту.
Учень/учениця застосовує вивчені означення і властивості до розв’язування задач, зокрема практичного змісту.