Опис завдання
У цій вправі ти потренуєшся встановлювати генетичні зв’язки між органічними сполуками. Це вміння дуже потрібне для підготовки до ЗНО з хімії, бо допомагає бачити логіку перетворень: як від найпростіших речовин (вуглеводнів) крок за кроком перейти до складніших класів сполук. Ти не просто вчиш назви, а вчишся «читати» органічну хімію як карту переходів.
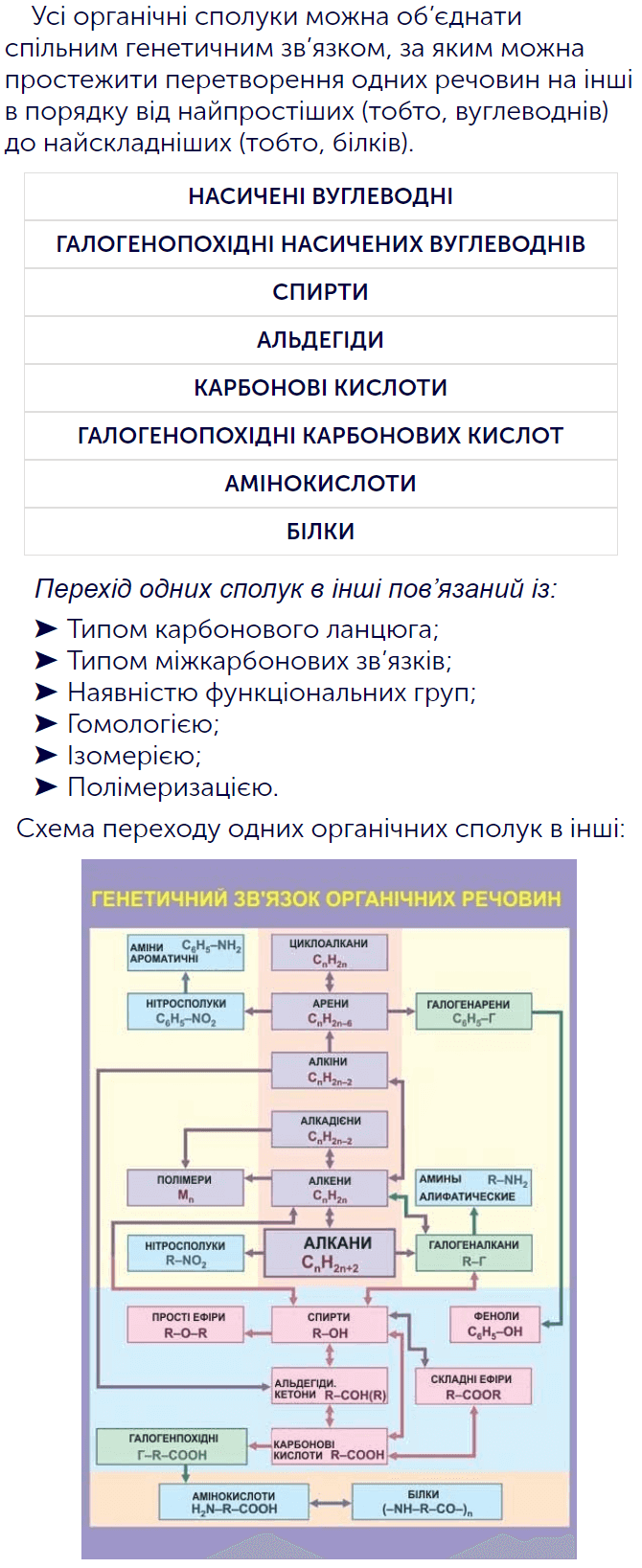
На схемі показано основні класи органічних речовин і напрямки перетворень між ними: насичені вуглеводні, галогенопохідні, спирти, альдегіди, карбонові кислоти, галогенопохідні карбонових кислот, амінокислоти та білки. Окремо подано ширшу схему, де зустрічаються алкани, алкени, алкіни, алкадієни, арени, полімери, нітросполуки, аміни, етери, феноли, естери та інші важливі групи. Твоя задача — навчитися пов’язувати ці «станції» між собою.
Під час виконання завдання ти будеш спиратися на ознаки, які визначають можливість переходу однієї сполуки в іншу: тип карбонового ланцюга, тип міжкарбонових зв’язків, наявність функціональних груп, а також явища гомології, ізомерії та полімеризації. Так ти швидко зрозумієш, чому, наприклад, спирти можуть переходити в альдегіди, а карбонові кислоти — давати похідні, з яких далі отримують амінокислоти й навіть білки.
- Для учня: тренуєш логічне мислення й повторюєш ключові класи органічних сполук.
- Для батьків: легко перевірити, чи дитина розуміє не лише формули, а й зв’язки між темами.
- Для вчителя: зручно використати як коротке узагальнення перед контрольними та підготовкою до ЗНО.
Працюй уважно: дивись, які функціональні групи з’являються або зникають, і як змінюється тип зв’язків у ланцюзі. Якщо ти навчишся будувати такі «маршрути перетворень», органічна хімія стане набагато зрозумілішою, а типові завдання ЗНО виконуватимуться швидше й упевненіше.
Пов'язані стандарти
Учень/учениця: формулює означення раціонального рівняння, рівняння-наслідку даного; розв'язує раціональні рівняння, які зводяться до лінійних; пояснює алгоритм графічного методу розв'язування раціональних рівнянь.
Учень/учениця: пояснює поняття: числова нерівність; доводить властивості числових нерівностей; знаходить об'єднання та переріз числових проміжків; зображує на числовій прямій множини, задані за допомогою нерівностей.
Учень/учениця: формулює означення синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника; записує та доводить основні тригонометричні тотожності; обчислює значення синуса, косинуса, тангенса і котангенса для кутів 30°, 45° і 60°.