Зовсім нещодавно на нашій платформі стартував 8 клас з математики. Сьогодні ми хочемо познайомити вас ближче із нашим новим курсом та розповісти про його найголовніші особливості. Тому швидше до справи!
Головне:
Новий курс призначений для учнів віком від 13 до 14 років. Він допоможе школярам сьомих, восьмих та дев’ятих класів покращити та поглибити свої знання з геометрії та алгебри.
Цей курс містить 335 завдань. Вони групуються на дві великі категорії: вправи з алгебри та геометрії. У складі кожного такого підкурсу завдання диференціюються за темами для кращого сприйняття. У рівні загалом 30 тем.
Всі завдання визначені стандартами МОН України для восьмого класу. Також є вправи, що відповідають ще й міжнародному стандарту Common Core. З їхньою допомогою учням вдасться ще більше поглибити розуміння відповідної теми.
Завдання тільки за міжнародними стандартами відмічені зеленими прапорцями, а такі, що присвячені більш глибокому вивченню теми, — помаранчевими.
Традиційно:
Кожна успішно пройдена тема означає нову нагороду. Це може бути логічна гра, розмальовка, лабіринт, пазл, судоку та, звісно, наліпки. До речі, в особистому кабінеті у кожного учня є своя статистика. Там можна побачити, скільки завдань вже виконано, скільки з них — правильно, які бали отримано та якого рейтингу досягнуто.
Така система дозволяє батькам та дітям контролювати власні успіхи та досягати ще більших результатів.
Отож, пропонуємо перейти до основних тем більш детально.
Алгебра:
В.13 Розв’язуємо степеневі рівняння

Розв’язання рівнянь — одна із найголовніших вправ в алгебрі, адже задіює всі можливі знання учня. Конкретно ця тема розглядає знаходження невідомого при діях зі степенями. Учень має вміти працювати з показниками, перетворювати їх, виконувати різноманітні арифметичні дії.
Для розв’язання подібного рівняння необхідно спочатку максимально спростити вираз, а вже потім знайти всі невідомі. Після того, як рішення знайдено, потрібно просто натиснути на правильний варіант та перейти до наступного завдання.
Ґ.5 Скорочуємо раціональні дроби

Під час проходження цього завдання учень потренує навичку роботи із дробами. Для того, щоб в подальшому легко та швидко працювати зі звичайними прикладами, восьмикласник має навчитися спрощувати чисельник та знаменник дробу до максимально можливих величин. Адже, якщо після цього потрібно буде підставити будь-яке число замість буквеного виразу, обчислення буде набагато швидшим.
Крім того, така вправа навчить школяра швидко орієнтуватися між початковою формою виразу та кінцевою, спрощеною. Щоб виконати завдання, необхідно відновити рівності правої та лівої частини, перетягнувши їх мишкою.
Ж.4 Графічний спосіб розв’язування системи рівнянь
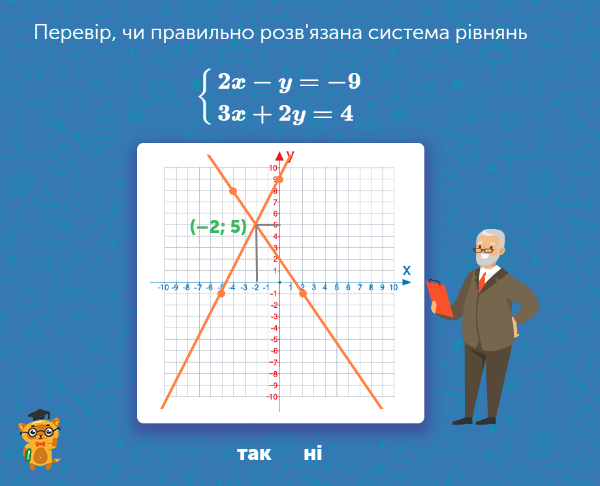
Окрім того, що восьмикласник має вміти вдало розв’язувати звичайні рівняння, а також системи рівнянь, він повинен знати, як знаходити розв’язки за допомогою графіку функцій.
Ця вправа поступово вводить дитину у це вміння. Адже учню доведеться просто порівняти записану систему рівнянь та запропоновані на екрані розв’язки. Для цього, замість х та у потрібно просто підставити відповідні значення точки.
У подальшому школяр має навчитися самостійно визначати, що за функція представлена перед ним та як вона буде відображатись на координатній площині. А от точки перетину цих двох функцій — це і є розв’язки системи рівняння.

Основне завдання нашої платформи — продемонструвати учням, де в житті можна застосувати набуті знання. Ця вправа націлена саме на це.
Перед учнем — повідомлення з банку, а саме — звичайна задача на відсотки. Однак, така ситуація може бути реальністю, тому дитині важливо навчитися вирішувати такі задачі хоча б в теорії.
Із цього завдання восьмикласник дізнається, що таке пеня, звідки вона з’являється та як вираховується. Щоб розв’язати задачу, потрібно вирахувати, яким числом є цей відсоток від першої суми. Потім результат слід помножити на кількість днів, яку нараховувалась пеня, а потім додати відповідь до початкової суми.
Н.1 Властивості подільності чисел

Знання основних теорій подільності дозволить учням простіше та швидше орієнтуватися у розв’язуванні та обчисленні виразів. Так, завдяки цим теоріям, восьмикласники зможуть швидко проаналізувати приклад та його майбутній результат.
У цьому завданні перед школярем будуть з’являтися як правильні, так і неправильні твердження щодо основних ознак подільності. Завдання учня — проаналізувати твердження та дати відповідь щодо їхньої правильності.
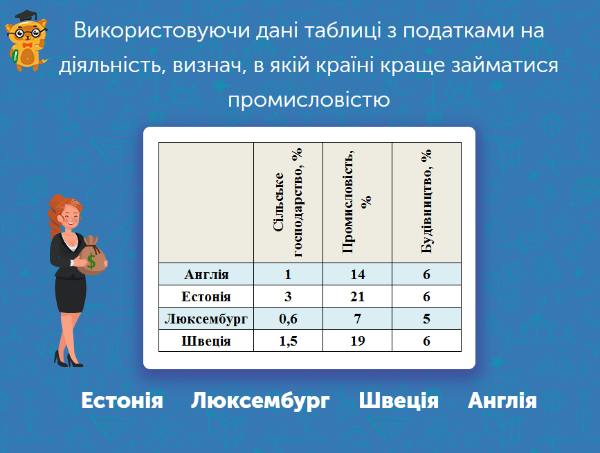
Подібна вправа є чудовою можливістю для того, щоб розвинути підприємницькі навички у дитини.
Перш за все, учень має вміти читати статистичні дані та діаграми. Завдяки цьому, він легко зрозуміє завдання та розв’яже його.
Ця вправа також тренує логіку дитини, розповість про цікаві факти щодо різних країн світу. Наприклад, після цього завдання учень дізнається, що найбільший відсоток на промисловість (порівняно з іншими 3-ма країнами) накладається в Естонії. Тому, якщо раптом доведеться обирати, чим займатися та в якій країні, восьмикласник зможе легко проаналізувати подану інформацію та зробити відповідні рішення.

Задачі є невід’ємною частиною будь-якої навчальної програми з математики. Вони розвивають логічне мислення та дозволяють на практиці застосувати набуті знання та навички.
Тема «Задачі на рух» тренує вміння школяра визначати швидкість транспорту, відстань, яку він пройшов, а також час, за який пройдено задану відстань. Крім того, для такого транспорту, як яхта, важливо враховувати ще й силу вітру, яка впливатиме й на швидкість яхти, й на час проходження певної відстані.
Конкретно у цій вправі, після аналізу заданих показників восьмикласник має вирахувати швидкість яхти та обрати один з трьох можливих варіантів.
П.9 Будуємо стовпчасті діаграми
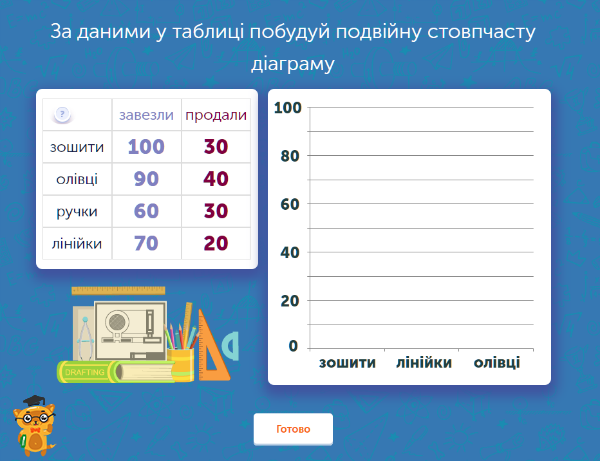
Статистика допомагає систематизувати та упорядкувати дані. Однак, для того, щоб зробити їх наочними, необхідно навчитися будувати діаграми. Восьмикласник вже добре знайомий із цим поняттям. Однак, у восьмому класі діаграми ускладнюються.
Зокрема, ця вправа просить від учня побудувати подвійну стовпчасту діаграму. У лівій частині є таблиця із заданими параметрами, праворуч — графік, на якому потрібно намалювати діаграму. Школяр аналізує інформацію, а потім логічно відображає її завдяки стовпчастій подвійній діаграмі.
Геометрія
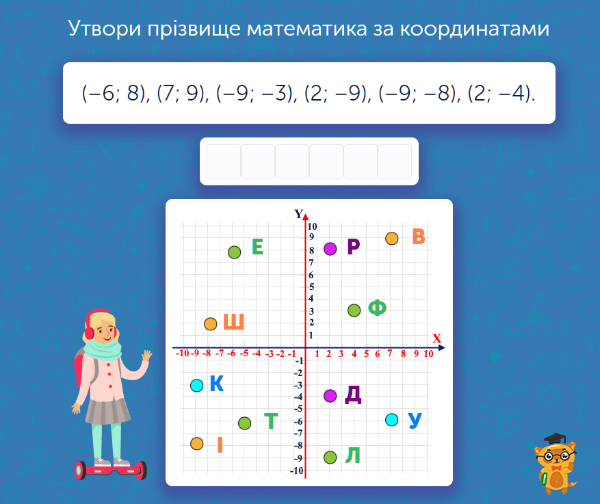
Перша тема, яка відкриває розділ з геометрії у восьмому класі стосується вивчення координатної площини. Учень згадає головні особливості роботи, навчиться відображати точки на координатній площині та будуватиме прості геометричні фігури.
Щоб вивчення цього розділу було не просто теоретичним та систематичним, а й пізнавальним та веселим, ми створили завдання «Вивчаємо математиків».
Восьмикласник побачить перед собою координати декількох точок (кожна точка — це частина прізвища математика). Після цього він має віднайти на координатній площині ці точки та з’ясувати, які літери сховались під ними. Коли всі літери будуть знайдені, школяр отримає ім’я справжнього математика!
Х.1 Гра «Яка фігура утворилася?»

Крім знайомства із двовимірними фігурами, восьмикласник дізнається про можливість їхньої трансформації. Зокрема, одна фігура може перетворюватися на іншу шляхом її обертання або іншої зміни відносно свого початкового положення.
Школярам доведеться добре попрацювати зі своєю уявою та фантазією, щоб дати точні відповіді на питання. А от у самому завданні формулюється ситуація, і необхідно уявити собі початкову фігуру та правильно визначити те, відносно чого відбувається обертання, щоб зрозуміти, яка фігура утворилася.
Щоб впоратись було простіше, під знаком питання є маленька підказка до завдання.
Ч.6 Тригонометричні співвідношення

Восьмикласник має чудово орієнтуватися у таких поняттях, як синус, косинус, тангенс та котангенс кутів прямокутного трикутника. Завдяки цим тригонометричним поняттям можна з легкістю дізнатися невідомі сторони або кути трикутника.
Знаходити невідомі елементи можна за допомогою перетворення формули, де є ці елементи, на правильні вирази з дробами, що означають співвідношення довжин потрібних сторін.
Зокрема, в цьому завданні учень має лише один відомий кут та довжину катета, що лежить навпроти нього. Обравши одну із тригонометричних теорем, учень швидко з’ясує, якою все-таки буде довжина невідомої гіпотенузи.
Щ.6 Розшукуємо фігуру за її описом

У процесі вивчення геометрії восьмого класу учень зустрінеться не тільки із двовимірними фігурами. Перед ним постануть й тривимірні. Один із розділів, який націлений на те, щоб пояснити дитині основні аспекти тривимірних фігур та надати теоретичну базу — це розділ «Розшукуємо фігуру за її описом».
Важливо, щоб школяр розумів: тривимірні фігури знаходяться у просторі, а не на площині. Тому вони мають набагато складніші параметри.
У цій вправі учень має прочитати визначення фігури та обрати ту, про яку це визначення написане. Таке завдання дозволить восьмикласнику легко орієнтуватися у фігурах та знати їхні головні особливості. В подальшому це вміння знадобиться для вирішення більш складних завдань та задач із тривимірними фігурами.
Ш.5 Знаходження невідомого кута трикутника
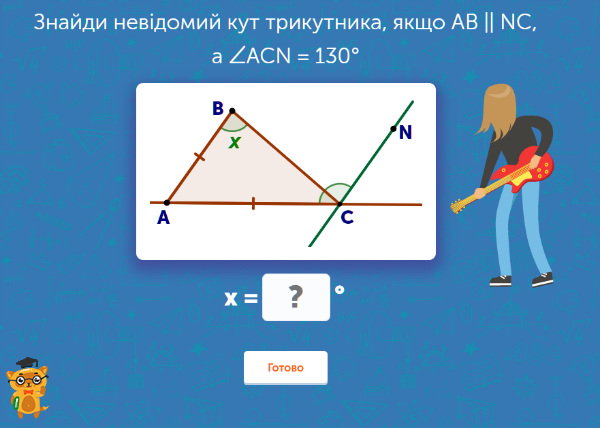
Знайти невідомий кут трикутника можна не лише через використання відомих його кутів, а й за допомогою прямої, яка проходить через точку, що належить його куту, поза межами фігури. Для цього необхідно знати усі властивості кутів та прямих, які проходять через них. Це можуть бути суміжні або відповідні кути, які допоможуть визначити градусну міру невідомих.
Конкретно в цій вправі учень має з’ясувати один із невідомих кутів трикутника, при тому, що через одну з його вершин проходить пряма, паралельна до однієї зі сторін даного трикутника. Відомий також один кут. Застосувавши властивості прямих, восьмикласник з легкістю прийде до правильної відповіді.

Завдяки тому, що учень знає формули для обчислення площ, периметрів та об’ємів, йому із легкістю будуть даватися звичайні життєві ситуації.
Зокрема, ця задача. В ній дитині доведеться застосувати свої знання щодо об’ємів тривимірних фігур, а саме — паралелепіпеду. У задачі надано довжини сторіни прямокутного паралелепіпеду, що наштовхне восьмикласника на вирішення завдання за правильною формулою.
Вправа ще раз продемонструє школяру, наскільки важливо вміти застосовувати свої знання на практиці.
Вивчення двовимірних фігур означає, що учень дізнається все про їхні основні властивості, а також зрозуміє, як застосовувати їх для вирішення реальних задач.
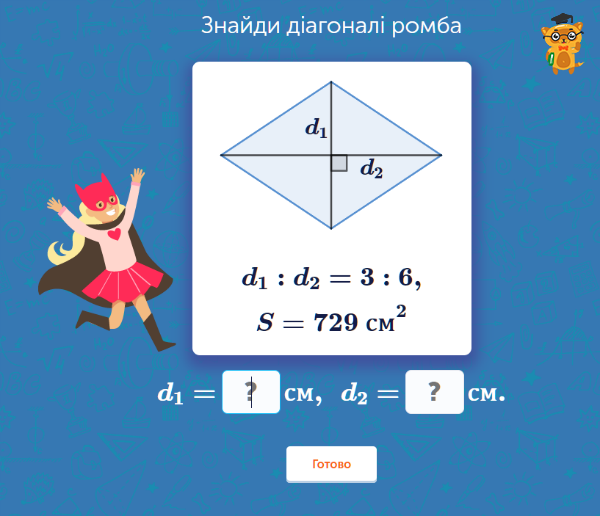
Тема «вивчення ромба» включає в себе таке поняття, як його площа. Знаходити площу ромба можна декількома варіантами. Однак, завдання восьмикласника полягає у тому, щоб поглянути на зображення та проаналізувати, які вихідні дані він має та яку формулу все-таки варто застосовувати у цьому конкретному випадку.
Ця вправа для обчислення площі ромба використовує інформацію про довжини його діагоналей. Знаючи співвідношення довжин цих відрізків та площу фігури, можна обчислити і самі ці сторони, використовуючи формулу як каркас рівняння. Надзвичайно просто, якщо знати, з якою формулою працювати!
На цьому ми пропонуємо завершити наш огляд. Насправді, у цьому рівні ще стільки всього цікавого, яскравого та пізнавального! Але, якщо розповідати про кожну вправу окремо, наш огляд затягнеться на справжнє невеличке видання :)
Сподіваємось, тепер у вас є певне уявлення щодо нового курсу. А щоб краще з ним познайомитись — заходьте на рівень та проходьте завдання!
Нехай щастить!