Ділення з остачею

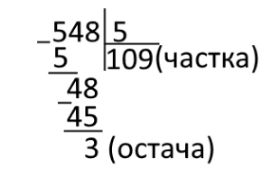
Певною мірою ділення є найскладнішою з чотирьох основних математичних дій. Справа в тому, що для доданків та множників немає ніяких обмежень, а єдине обмеження для класичного віднімання – це, щоб зменшуване було більшим за відʼємник. З діленням все не так. Далеко не кожне число можна поділити на інше. При чому, чим більшим є дільник, тим менше чисел можна на нього розділити. Наприклад, на двійку діляться всі парні числа, а це рівно половина з усієї їхньої безкінечності. А от на вісімку вже можна розділити набагато менше чисел. Фактично, кратність числа іншому визначається наступним чином: якщо теоретичне ділене може бути утворене шляхом множення теоретичного дільника на будь-яке інше число, то ділення можливе. Наприклад, «12» можна розділити на «4», адже відомо, що «4 х 3» і дає цю «12». Проте іноді треба виконати дію ділення тих чисел, які не підходять одне одному. В такому випадку залишається остача. Відбувається це таким чином: необхідно знайти найближче менше до діленого число, яке підходить для того, щоб його розділили на дільник без остачі. Далі виконується це ділення, а поряд з ним, у круглих дужках, позначається різниця між справжнім діленим та цим числом. Наприклад, якщо треба розділити «14» на «4», то ту ж саму «12» ділять на четвірку, а в дужках результат віднімання «12» від «14», і результат виглядає так: «3 (2)». У ході виконання цього завдання дитина виконуватиме ділення з остачею за цим правилом, проте  ділене та дільник будуть вже більшими числами, що ускладнює процес. Отже, учень виконує порозрядне ділення, шукаючи у великому числі ті частини, які можна розділити на дільник, а потім, не забуваючи про розрядність частки, вписує у круглі дужки остачу – різницю першого діленого з тим, яке було використано.