Опис завдання
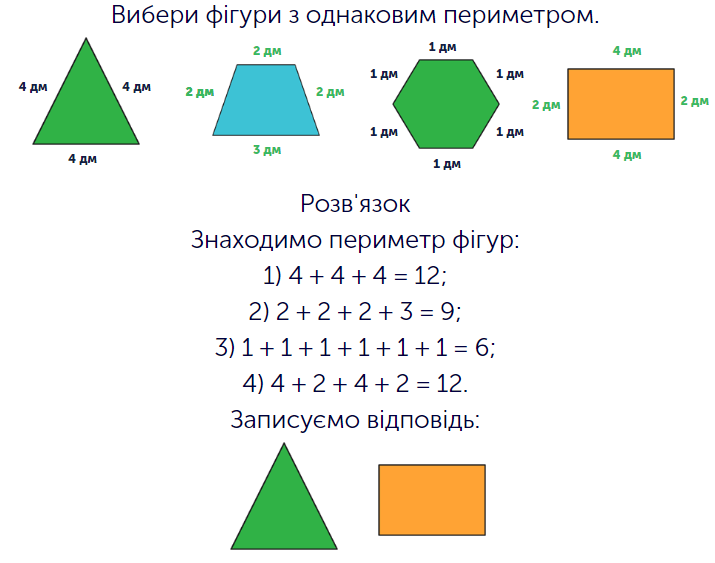
Формула знаходження периметра завжди одна й та сама незалежно від того, про яку фігуру йде мова: треба просто додати між собою всі довжини сторін. Це наводить на висновок, що однаковим периметр може бути й у фігур, які належать до абсолютно різних видів і навіть візуально відрізняються за розмірами, принаймні на перший погляд. У ході виконання цього завдання дитина пересвідчиться у цьому. На екрані перед учнем міститься зображення цілого ряду фігур. Всі вони належать до різних видів, а крім того ще й виповнені у різний колір. Довжину їхніх сторін відомо, отже, залишається лише обчислити периметр кожної фігури. Завдання, яке ставиться перед дитиною на кожному з рівнів, залишається одним і тим самим – вибрати ту пару фігур, які мають однаковий периметр. Коли учень це робить, то проходить на наступний етап завдання, де треба буде виконати аналогічну послідовність дій. Ця вправа демонструє не лише те, що багатокутники можуть бути подібні між собою всупереч належності до різних видів, а й те, як можна використати знання периметра. Існує безліч практичних задач, а також цілком життєвих ситуацій, коли необхідно дізнатись периметр замкненої (тобто територіально обмеженої) ділянки, яка може мати нетипову форму, після чого порівняти її з довжиною кордонів іншої подібної ділянки іншої форми. Таким чином, це завдання, як і кілька попередніх, переводять роботу з периметром у дещо більш практичну площину. Крім того, дитина на кожному етапі працює відразу з цілим рядом фігур, що стимулює її докладати більше зусиль для концентрації, тримати в пам’яті більший об’єм інформації та вчитись водночас з цим виконувати послідовність математичних дій з певними числами.