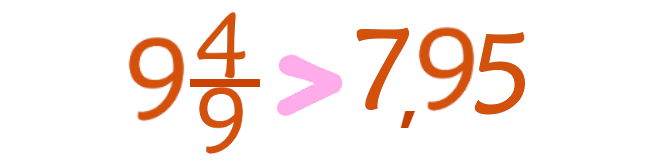Гра «Вгадай знак»

Порівняння дробів – досить цікавий процес, адже кожен дріб являє собою окремий випадок розділення умовного цілого на частинки, тож порівняти їх не так вже й просто. Це стосується і порівняння дробів, що належать до одного виду, і тим паче випадків, коли треба порівнювати звичайний дріб з десятковим. У ході виконання цього завдання школяр тренуватиметься в цьому. На екрані перед дитиною міститься зображення двох чисел: мішаного і десяткового. Цілий компонент їх обох є однаковим, тоді як у дробі частини у них зовсім різні. Однак, з першого погляд визначити, який дріб є більшим, складніше, ніж може здатись. Наприклад, якщо порівняти дріб «0,3499» з дробом з одиницею в якості чисельника та двійкою в якості знаменника, вдаватись до звичайного по цифрового порівняння не можна. Натомість важливо розуміти, що означає той чи інший дріб. В наведеному прикладі звичайний дріб – це одна друга від одиниці, тобто її половина. Якщо це виразити у десятковому дробі, то виглядатиме він «0,5», а це більше, ніж «0,3499». Випадки, з якими стикатиметься учень у ході виконання цієї вправи, складніші. В чисельниках і знаменниках будуть більші числа, як і після коми в десяткових числах. Щоб виконати порівняння не «на око», а точно, необхідно десяткове число перевести у мішаний дріб, де знаменник вказується розрядом. Наприклад, «4,56» можна перетворити на мішане число з четвіркою на місці цілих чисел ті дробом зі знаменником, що дорівнюватиме «100», адже розряд десяткового числа так і звучав: «пʼятдесят шість сотих». Коли дитина перетворює десяткове число на мішане, необхідно також вдатись до скорочень з обох боків, після чого або привести дроби до спільного знаменника, або вже, якщо відповідь очевидна, порівнювати їх після цього скорочення.