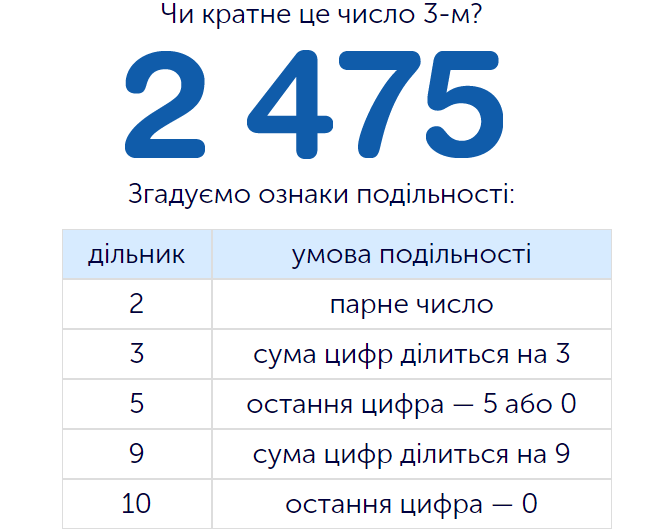
Опис завдання
Особливість теми кратності полягає у тому, що завдяки ній дитина навчиться швидко визначати, чи ділиться те чи інше число на певний дільник. Існує набір ознак, які присвячені цьому, і учень, дійшовши до цього етапу, вже знає ці ознаки. Наприклад, на двійку ділиться будь-яке парне число; певне число є кратним трійці тоді, коли сума цифр, що входять до його складу ділиться на трійку без остачі; кратними пʼятірці є лише ті числа, що закінчуються на нуль або «5» тощо. У ході виконання цього завдання дитина закріпить знання цих ознак подільності. На екрані перед учнем міститься зображення числа – нового для кожного етапу завдання. Над ним вказується число і задається питання: чи є центральне кратним числом для того, яке подається зверху. Звісно, дитина, щоб перевірити це, може просто розділити одне на друге, однак, оскільки у центрі екрані завжди багатоцифрове число, яке може сягати десятків тисяч, робити це не обовʼязково. Значно простіше скористатись ознаками подільності, які школяр вже знає. По боках від числа є пара персонажів, один вважає, що центральне число ділиться на те, яке вказане у завданні, інший – що не ділиться. Дитина має вибрати героя, який є правим у цій суперечці та натиснути на відповідний символ, який тримає один із них. Після цього школяр проходить на наступний етап, де аналогічним чином треба опрацювати інше число, перевіривши його кратність до іншого дільника. При цьому ніяких додаткових підказок не буде, і якщо дитина забула ознаки подільності, єдиний спосіб перевірити себе – це виконати ділення. Таким чином, ця вправа водночас дозволяє і закріпити в памʼяті названі ознаки, і потренувати вміння ділити великі числа на одноцифрові дільники.
Пов'язані стандарти
Учень/учениця: наводить приклади простих і складених чисел, парних і непарних чисел.
Учень/учениця: розрізняє прості і складені числа, дільники і кратні натурального числа.
Учень/учениця: формулює означення понять: дільник, кратне, просте число, складене число, спільний дільник; знає ознаки подільності на 2, 3, 5, 9, 10.