Опис завдання
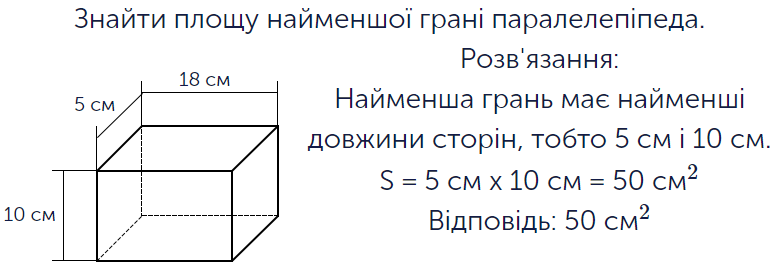
Геометричні фігури, які належать до так званих тривимірних, або об’ємних, мають більше елементів, ніж звичайні двовимірні. Крім того, і це навіть важливіше, вони й сприймаються по-іншому. Наприклад, це стосується і того, як знаходити умовний «розмір» фігури. У двовимірних фігур все просто. Є поняття площі та периметру. Площа – це те, який розмір «поверхні» площини займає фігура, а периметр – довжина всіх її сторін. Тривимірні фігури теж мають поняття площі, однак воно сприймається вже по-іншому через те, що ці фігури знаходяться у просторі й мають глибину. Вона ж, ця глибина, тобто частина простору, що займається фігурою, називається об’ємом. У ході виконання цього завдання дитина виконуватиме своєрідні графічні задачки на знаходження площі або об’єму тривимірної фігури. На кожному етапі перед учнем знаходитиметься зображення лише одного виду таких фігур, а саме – прямокутного паралелепіпеда. Особливість цієї фігури у тому, що вона будується виключно з прямокутників. Дитині на малюнку надається довжина його ребер. Над малюнком міститься питання з уточненням, що саме треба знайти. Скажімо, периметр найбільшої або найменшої грані фігури. Це лаконічне формулювання означає досить об’ємний алгоритм дій. Наприклад, якщо дитина має знайти саме це, то необхідно спочатку визначитись з об’єктом опрацювання. Найбільша грань у цьому випадку – найбільший прямокутник. Дитина шукає його по значенню ребер паралелепіпеда. Далі залишається просто перемножити довжину ширини грані на її довжину – як і у випадку із знаходженням площі прямокутника. Варіанти відповіді подаються під малюнком. Коли дитина вибирає один правильний, то проходить на наступний етап.
Пов'язані стандарти
Куб з довжиною бокової сторони 1, що називається "кубічною одиницею", має "один кубічний блок" об'єму, і може використовуватися для вимірювання об'єму.
Знаходити об’єм правильної прямокутної призми із цілими числами довжин сторін, наповнюючи її кубічними одиницями, і показувати, що об’єм був би таким самим, якщо його було б знайдено шляхом множення висоти та площі основи. Представляти цілі результати як об’єм, наприклад, щоб відобразити асоціативну властивість множення
Знаходити об’єми твердих фігур, які складаються з двох непересічних правильних прямокутних призм, додавши обсяги непересічних частин, застосовуючи цю техніку для вирішення практичних задач.