Опис завдання
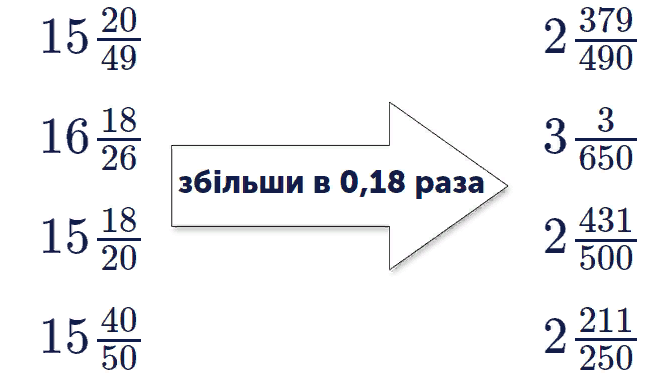
Множення та ділення у випадку з дробами може давати досить неочікуваний результат. Наприклад, якщо помножити на десятковий дріб, то добуток може бути меншим, ніж перший множник, а якщо розділити, то частка більша, ніж ділене.
У процесі виконання цього завдання дитині пропонується відчути себе учнем могутнього чарівника, який перетворює дроби. Перед учнем міститься зображення двох робочих зон. В обох є дроби. Між ними — чарівник, що перетворює елементи одного ряду на елементи іншого за допомогою множника, спільного для них. Наприклад, таким множином може бути число «0,2», і тоді всі дроби в першій групі треба помножити на це число. Відповідно дроби в іншій групі — це результат цього множення. Однак спочатку ці числа перебувають в хаотичному порядку, і завдання, яке ставиться перед учнем, полягає в тому, щоб перемістити елементи іншої групи таким чином, щоб вони були навпроти перших множників.
Для цього учню необхідно повторити множення з кожною парою чисел, що розвиває уважність у роботі з дробами.