Опис завдання
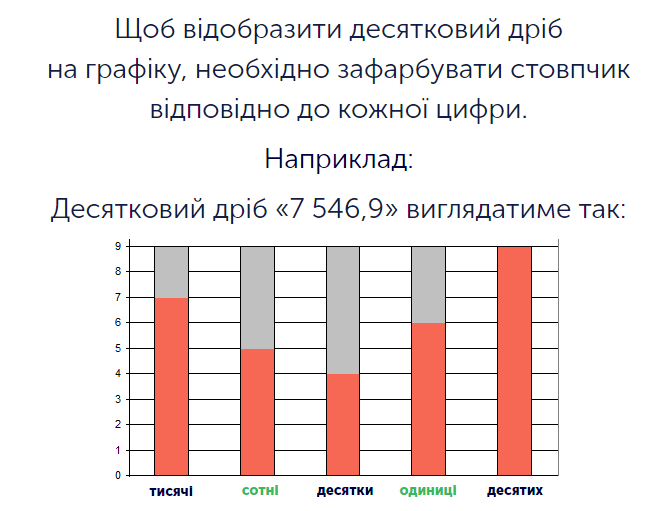
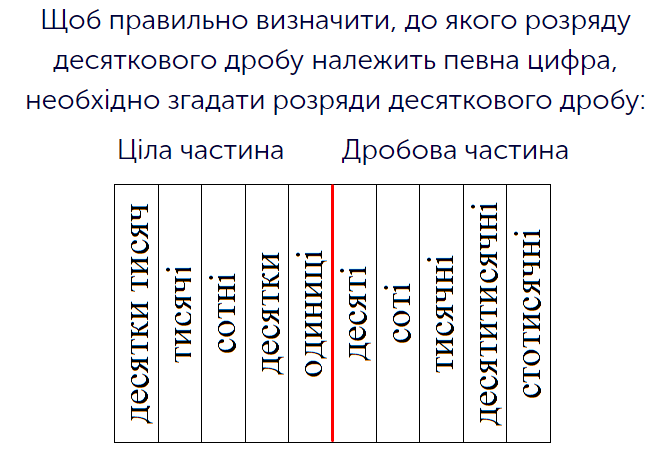
Існує кілька різновидів дробів: звичайний дріб із чисельником та знаменником, неправильний дріб, де знаменник менший, ніж чисельник, мішане число, яке містить також і цілий компонент. Однак, досить істотно виділяється десятковий дріб. Справа в тому, що він досить зручно та ефективно поєднується з цілим числом, утворюючи структури на кшталт «12,451» або «1,49» тощо. Як ціла, так і дробова частини мають свої розряди. З розрядами цілих чисел дитина знайома з першого класу. Розряди дробових визначаються знаменником, який мав би бути, якби ці дроби перевести у формат звичайних. Відразу після коми знаходиться розряд десятих, далі – сотих, потім – тисячних, десятитисячних, ста тисячних – і так далі, до безкінечності. Відповідно, десяткові дроби треба вміти правильно читати та зображати за описом, чому й присвячено це завдання. Якщо у ході виконання попередньої вправи дитина тренувалась відтворювати дріб за зображенням, то тепер необхідно буде виконати зворотну дію – зобразити графічно десятковий дріб, який подається числом. На екрані перед учнем міститься зображення стовпчастого графіку, де кожен стовпчик має назву, відповідну цілому або дробовому розряду. Над цим графіком міститься зображення дробу, який треба опрацювати. Школяр читає дріб, після чого аналізує кожен його розряд окремо, ставлячи висоту стовпчиків з назвами цих розрядів на відповідну висоту. Наприклад, якщо дріб «14,4», то стовпчик, що показує розряд десятків має бути на висоті одиниці, а стовпчик, який відповідає за розряд десятих – на висоті четвірки. Таким чином, хоча при називанні дробу цілу та дробову частини називаються двома числами, при їх графічному зображенні кожен розряд відокремлюється.
Пов'язані стандарти
Учень/учениця: наводить приклади скінченних та нескінченних періодичних десяткових дробів.
Учень/учениця: розуміє правила порівняння дробів.
Учень/учениця: розуміє правила знаходження дробу від числа та числа за його дробом.